Atomic Theory

The Grand Unified Theory of Classical Physics – Atomic Theory Resources

 

 

View the Atomic Physics Slideshow (PDF)

View the book: Volume 1: Atomic Physics.

View accompanying spreadsheets12:
Stark Effect
State Lifetimes and Line Intensities for 1-Electron Atom
QED Calculations
Helium Excited States
H- and Hydrino H-
One Through Ten Electron Atoms
Eleven Through Twenty Electron Atoms

View Discussions of Canonical Experiments:

Electron Double-Slit Experiment
Aspect Experiment

View Related Papers:

Exact Classical Quantum Mechanical Solutions for Atomic Helium Which Predicts Conjugate Parameters from a Unique Solution for the First Time – R.L. Mills, Physics Essays, Vol. 21(2), (2008), 103–141.

View accompanying spreadsheets.

The Fallacy of Feynman’s Argument on the Stability of the Hydrogen Atom According to Quantum Mechanics – R.L. Mills, Annales de la Fondation Louis de Broglie, Vol. 30, No. 2, (2005), pp. 129-151.

Exact Classical Quantum Mechanical Solutions for One- Through Twenty-Electron Atoms – R.L. Mills, Physics Essays, Vol. 18, No. 3, September, (2005), pp. 321–361.

View accompanying spreadsheets.

Classical Quantum Mechanics – R. Mills, Physics Essays, Vol. 16, No. 4, December (2003), pp. 433-498.

Physical Solutions of the Nature of the Atom, Photon, and Their Interactions to Form Excited and Predicted Hydrino States – R. Mills, Physics Essays, Vol. 20, No.4, (2007) 403.

View Related Computation Files: Note: Some files may require Mathematica Viewer.

Modeling the Analytical Equations to Generate the Atomic Orbital Current-Vector Field (See Ch.1) – pdf or zip of .nb

Analytical Equations to Generate the Free Electron Current Vector Field and the Angular Momentum Density Function (See App. IV) – pdf or zip of .nb

Electric Potential and Field of the Free Electron, Semi-Analytic Approach – pdf or zip of .nb

Electric Potential and Field of the Free Electron, Code Summary and Visualization – pdf or zip of .nb

Appendix V: Analytical Equation Derivation of the Photon Electric and Magnetic Fields (See App. V) – pdf or zip of .nb

Modeling of the Larmor Precession – pdf or zip of .nb

Modeling of the Free Electron – pdf or zip of .nb

Modeling of the Modulation Functions – pdf or zip of .nb

View Related Visualizations:

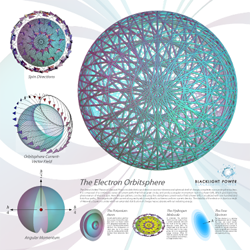
Orbitsphere Poster
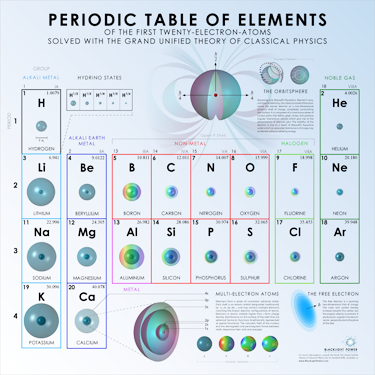
Electron Atomic Orbital Poster
Image | PDF

Electron Atomic Orbital Current Pattern (Ch. 1 )

The bound electron (the electron atomic orbital) is composed of a continuous distribution of great-circle current loops. The distribution is constructed such that it results in two angular momentum vectors, giving rise to the phenomenon of electron spin. Once achieved, this distribution is unique according to Maxwell’s Equations.

H Distribution Renderer

This stand-alone executable allows the user to numerically calculate and render the charge distribution profile and angular momentum projections of the hydrogen atom, both unnormalized and normalized.


Point-Visualization
of the BECVF
Rotating Viewpoint
of the BECVF
3D interactive figure
of the BECV

Convolution to generate
uniform function
(See Fig. 1.12)
Convolution to generate
uniform function
(See Fig. 1.12)
Uniform function
(See Fig. 1.12)

High-quality view of BECVF
(See Fig 1.5)
High-quality view of
uniform function
(See Fig 1.12)
Larmor precession of a
hydrogen atom in a
magnetic field.

Modulation Functions (Ch. 1 )

Below: Atomic Orbitals (AO’s) are surface charge density waves on the electron atomic orbital that spin harmonically about the z-axis. Quantum mechanics interprets these as probability-density lobes.


Px or Py orbital
(See Fig. 1.2)
View animation
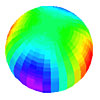Dx^2-y^2 orbital
(See Fig. 1.2)
View animation
Dxz or Dyz orbital
(See Fig. 1.2)
View animation

Excited States (Ch. 2 )

Below: Excited states form larger, concentric atomic orbitals with modulation functions. A radial dipole moment makes them unstable.


Photon absorption to
form an excited state.
Px or Py excited state
(brightness corresponds
to photon field strength)
(See Fig. 2.1)		  

The Free Electron (Ch. 3 )

Below: Free electrons form planar disks of moving charge in the plane perpendicular to their angular momentum axis. The angular velocity is constant, but the charge and current magnitude fall to zero at the edge of the disk.


Free electron
(See Fig. 3.2A)
View animation or
Precession of a free
electron in a magnetic field
(See Fig. 3.8)
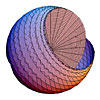Convolution of a free
electron in a magnetic field
(See Fig. 3.8)		  

Electron Ionization: Spherical to Plane Wave Boundary Condition Concept (See Fig. 2.2)
Electron Binding and Ionization (also see Photon absorption to form an excited state)
Simulation of Electron Binding and Ionization with Photon Mediated Transitions
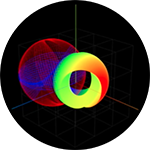Simulation of Photon Absorption by a Free Electron

The Photon (Ch. 4 )

Below: The photon is a distribution of electric and magnetic field lines.


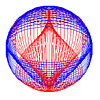Linearly polarized photon
(See Fig. 4.7)		 Photon Absorption

Classical Photon Scattering (Ch. 8 )


Classical photon
diffraction
(See Fig. 8.1)

Left: In the photon double-slit experiment, the impinging photon’s electric and magnetic fields give rise to currents at both slits (blue). The currents then reemit the photon, and the variation of intensity in the far field is due to the conservation of angular momentum of the source currents. There is no constructive or destructive interference of electromagnetic fields.

Classical Electron Scattering (Ch. 8 )
Below: For an online discussion of this topic, view the Electron Double-Slit Experiment page.


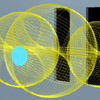Classical electron
diffraction
(See Fig. 8.9)
Classical electron
diffraction – top view
(See Fig. 8.9)		  

Multi-Electron Atoms


The potassium atom

Left: Multi-electron atoms consist of concentric electron atomic orbitals, one corresponding to each atomic orbital.